Fonction exponentielle

Introduction

De nombreux phénomènes physiques ou économiques simples peuvent être modélisés par une fonction $f$ vérifiant, pour tout réel $x$ d'un intervalle $I$ , $f' (x) = k \times f (x)$ où $k$ est un coefficient réel.

D'où l'importance pratique des équations différentielles du type

y' = k y

avec

k

constante réelle.

Exemple de la décroissance radioactive :

On admet que dans les corps radioactifs, la proportion de noyaux qui se désintègrent pendant une durée de temps $δ t$ est proportionnelle à cette durée. L'évolution du nombre $N (t)$ de noyaux du corps au temps $t$ se modélise alors par la loi suivante, où 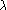lambda est une constante positive, dépendant seulement du corps radioactif :

\frac{N (t) - N (t + δ t)}{N (t)} = λ δ t

ce qui équivaut à

\frac{N (t + δ t) - N (t)}{δ t} = - λ N (t)

pour tout

t \in ℝ^{+}

.
Pour de petits intervalles de temps

δ t

(

δ t \to 0

), on assimile l'expression de gauche au nombre dérivé

N' (t)

. La loi prend la forme d'une équation différentielle, càd une équation qui met en relation la fonction

N

et sa fonction dérivée

N'

N' (t) \approx \frac{N (t + δ t) - N (t)}{δ t}

d'où

N' (t) = - λ N (t)

pour tout

t \in ℝ^{+}

. Ainsi la fonction

N

est solution de l'équation différentielle

y' = - λ y

sur

ℝ^{+}

Il est assez facile de montrer que si l'on sait résoudre l'équation différentielle

y' = k y

avec

k = 1

, alors on sait résoudre les équations

y' = k y

avec

k

quelconque.

On va s'intéresser plus particulièrement à l'équation

y' = y

et l'on va chercher les éventuelles solutions de cette équation différentielle en imposant comme condition initiale

y (0) = 1

Plan

1. Définitions

2. Propriétés algébriques

3. Variations et Limites

4. Exponentielle d'une fonction u : composée exp(u)

5. Logarithme d'un réel strictement positif

6. Equations et inéquations avec exponentielles

7. Primitives

1. Définitions

Conjecture d'existence : Grâce à la méthode d'Euler on conjecture l'existence d'une fonction

f

dérivable sur

telle que

f' = f

f (0) = 1

Lemme : Si

f

est une solution de l'équation différentielle

y' = y

sous la condition initiale

y (0) = 1

, alors pour tout réel

x

on a

f (x) f (- x) = 1

. Par suite la fonction

f

ne s'annule pas sur

Démonstration : On pose

h : x \mapsto f (x) f (- x)

. On montre que h est dérivable sur

et que pour tout réel

x

on a

h' (x) = 0

. La fonction

h

est donc constante. Or pour

x = 0

, on a

h (0) = 1

, d'où

f (x) f (- x) = 1

quel que soit le réel

x

Propriété d'unicité : Si

f

g

sont solutions de l'équation de l'équation différentielle

y' = y

sous la condition initiale

y (0) = 1

, alors

f = g

Démonstration : Le quotient

ϕ = \frac{f}{g}

est défini sur

puisque

g

ne s'annule pas (cf. Lemme) et dérivable sur

comme produit de fonctions dérivables. On montre alors que

ϕ' (x) = 0

pour tout réel

x

. Donc

est une fonction constante. Or pour

x = 0

, on a

ϕ (0) = 1

, d'où

f (x) = g (x)

quel que soit le réel

x

Définition :

On appelle fonction exponentielle, et on note exp, l'unique fonction dérivable sur $ℝ$ solution de l'équation différentielle $y' = y$ et vérifiant la condition initiale $y (0) = 1$ .

On appelle nombre de Neper, et on note e, l'image de 1 par la fonction exponentielle. On a donc : e = exp(1).

2. Propriétés algébriques

Lemme : Pour tout réel $x$ on a : $\exp (x) \times \exp (- x) = 1$ .
On en déduit que la fonction exponentielle ne s'annule pas sur .

Démonstration : on montre que la fonction

h : x \mapsto \exp (x) \times \exp (- x)

est dérivable sur

et que

h' (x) = 0

pour tout réel

x

; on en déduit que la fonction

h

est constante ; or pour

x = 0

on a

h (0) = 1

Théorème :
Pour tous réels

x

y

on a :

\exp (x + y) = \exp (x) \times \exp (- x)

Pour tout réel

x

et tout entier relatif n on a :

\exp (n \times x) = \exp (x)^{n} = e^{n}

Démonstration :
Pour un réel

y

quelconque fixé, on montre que la fonction

h : x \mapsto \frac{\exp (x + y)}{\exp (x) \times \exp (y)}

est dérivable sur

et que

h' (x) = 0

pour tout réel

x

; on en déduit que la fonction

h

est constante ; or pour

x = 0

on a

h (0) = 1

.
La seconde égalité se démontre d'abord par récurrence sur

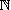. On la prolonge à

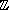sachant que

\exp (- x) = \frac{1}{\exp (x)}

(cf. Lemme).

Notation puissance : La fonction exponentielle prolonge aux réels les règles usuelles des exposants entiers.
Pour tout entier relatif n on a en effet : $\exp (n) = \exp (1 \times n) = \exp (1)^{n} = e^{n}$ .

On étend la notation puissance à tout réel

x

: $\exp (x) = e^{x}$ .

Pour tous réels $x$ et $y$ , on a donc les règles suivantes :

$e^{0} = 1$	$e^{1} = e$
$e^{x + y} = e^{x} \times e^{y}$	$e^{- x} = \frac{1}{e^{x}}$
${(e^{x})}^{y} = e^{x \times y}$	$e^{x - y} = \frac{e^{x}}{e^{y}}$

Propriété : Pour tout réel

x

on a :

\sqrt{e^{x}} = e^{x / 2}

Démonstration : d'après les propriétés algébriques de la fonction exp on a :

(e^{x / 2})^{2} = e^{2 \times x / 2} = e^{x}

Donc

e^{x / 2}

est un réel positif dont le carré est égal à

e^{x}

; c'est donc la racine carrée de

e^{x}

Le nombre e est un irrationnel, comme

\sqrt{2}

. Sa valeur exacte c'est e !

Dans un calcul exact, on exprimera donc le résultat en fonction de e.
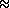Pour un calcul approché, on utilisera une approximation : e approx

2,7182818...

Exercices :
Notation puissance
Réécriture sous forme d'une seule exponentielle (1)
Réécriture sous forme d'une seule exponentielle (2)

3. Variations et Limites

Sens de variation

Par définition, la fonction exponentielle est dérivable sur

et sa fonction dérivée est identique à elle-même. pour tout réel

x

, on a

\exp' (x) = \exp (x) = e^{x}

Lemme : La fonction exponentielle prend des valeurs strictement positives : pour tout réel

x

, on a

e^{x} > 0

Démonstration : Pour tout réel

x

on peut écrire

\exp (x) = \exp (2 \times \frac{x}{2}) = \exp (\frac{x}{2})^{2}

. Or le carré d'un réel est un nombre positif ou nul. Par ailleurs on sait que la fonction exponentielle ne s'annule pas sur

. Donc, la fonction exponentielle est strictement positive sur

Thérorème : La fonction exponentielle est une fonction strictement croissante sur

. Elle réalise une bijection de

sur

ℝ^{+ *}

Démonstration : conséquence immédiate des deux propriétés précédentes.

Position relative avec la tangente à l'origine

La tangente à la courbe de la fonction exponentielle au point d'abscisse 0 a pour équation $y = x + 1$ .

Propriété : La courbe de la fonction exponentielle est entièrement située au dessus de sa tangente à l'origine : pour tout réel

x

, on a

x + 1 \leq e^{x}

Démonstration : On étudie le sens de variation de la fonction

ϕ : x \mapsto e^{x} - (x + 1)

et on montre que phi

atteint un minimum en

x = 0

. Or la valeur minimale de phi

est 0. Par suite les valeurs

ϕ (x)

sont toutes positives ou nulles, quel que soit le réel

x

Limites à l'infini

Thérorème :

\lim_{x \to + ∞} e^{x} = + ∞

\lim_{x \to - ∞} e^{x} = 0

Démonstration :
Limite en

+ ∞

: On sait que pour tout réel

x

x + 1 \leq e^{x}

. Or

\lim_{x \to + ∞} x + 1 = + ∞

donc

\lim_{x \to + ∞} e^{x} = + ∞

(théorème de comparaison pour les limites).
Limite en

- ∞

: On sait que pour tout

x

e^{x} = \frac{1}{e^{- x}}

. Or

\lim_{x \to - ∞} e^{- x} = \lim_{t \to + ∞} e^{t} = + ∞

, donc par inverse

\lim_{x \to - ∞} \frac{1}{e^{- x}} = 0

. D'où

\lim_{x \to - ∞} e^{x} = 0

La courbe de la fonction exponentielle admet l'axe des abscisses comme asymptote horizontale en

- ∞

Croissances comparée entre $e^{x}$ et $x^{n}$
En $+ ∞$ la fonction exponentielle croît beaucoup plus vite que les fonctions puissance $x \mapsto x^{n}$ .

Théorème (croissance comparée) : Pour tout entier naturel

n

\lim_{x \to + ∞} \frac{e^{x}}{x^{n}} = + ∞

- ∞

l'exponentielle de

x

est un infini petit qui l'emporte sur toute puissance entière de

x

Théorème (croissance comparée) : Pour tout entier naturel

n

\lim_{x \to - ∞} x^{n} e^{x} = 0

On mémorise ces propriétés en disant que " l'exponentielle l'emporte sur les puissances ".

Courbes respectives sur [-3 , 4] de la fonction exp et de la fonction carré

Exercice :

Choisir des exercices sur les limites.

4. Exponentielle d'une fonction u : composée exp(u)

Soit

u

une fonction définie et dérivable sur un intervalle

I

La composée

\exp \circ u

est la fonction définie sur

I

par :

\exp \circ u (x) = \exp (u (x)) = e^{u (x)}

.
On la note indifféremment

\exp \circ u

e^{u}

u

est dérivable sur

I

alors la fonction composée

e^{u}

est dérivable sur

I

et l'on a la formule de dérivation :

Théorème (dérivée d'une exponentielle) : Si la fonction

u

est dérivable sur

I

alors la composée

e^{u}

l'est aussi et :

(e^{u})' = u' \times e^{u}

C'est à dire, pour tout réel

x \in I

(e^{u})' (x) = u' (x) \times e^{u (x)}

Si $f$ est définie sur par $f (x) = e^{- x}$ , alors pour tout réel $x$ , on a $f' (x) = - e^{- x}$ .

Exemples (cliquer sur l'icône pour changer les données) :
Soit $f$ la fonction définie sur par $f (x) = e^{}$ .
$f = e^{u}$ avec $u : x \mapsto$ . $f$ est dérivable sur et, pour tout réel $x$ on a : $f' (x) = - e^{}$ .

Exercices :

Calculer la dérivée d'une composée exp(u)
Calculer la limite d'une composée exp(u)
Etude d'une fonction du type \(x \mapsto (a x+b)e^{kx})
Etude d'une fonction du type \(x \mapsto a x+b + e^{kx})

5. Logarithme d'un réel strictement positif

On a vu en 3. que la fonction exponentielle réalise une bijection de

sur

ℝ +^{*}

. Elle admet donc une bijection réciproque, définie sur

ℝ +^{*}

et à valeurs dans

Ainsi, tout réel strictement positif

b

admet un unique antécédent

a

par la fonction exponentielle. On nomme cet antécédent le logarithme népérien de

b

et on le note

\ln (b)

\ln b

L'équation

e^{x} = b

, où

b > 0

, admet une solution unique

x = \ln (b)

Définition : On appelle fonction logarithme, et on note

\ln

, la bijection réciproque de la fonction exponentielle.

Conséquences immédiates : La fonction

\ln

est définie sur

ℝ +^{*}

et prend ses valeurs dans

ℝ

.
On a :

\ln (1) = 0

\ln (e) = 1

Propriétés : Les fonctions

\ln

\exp

étant bijections réciproques l'une de l'autre on a :

pour tout réel $x$ , $\ln (e^{x}) = x$
pour tout réel $x > 0$ , $e^{\ln (x)} = x$
pour tout réel $x$ et pour tout réel $y > 0$ , $e^{x} = y \Leftrightarrow x = \ln (y)$
les courbes respectives des fonctions exp et ln sont symétriques l'une de l'autre par rapport à la diagonale d'équation $y = x$

NB : Le logarithme d'un réel strictement négatif n'est pas défini !

Exercice :

Simplifier une expression

6. Equations et inéquations avec exponentielles

Les équations ou inéquations suivantes sont résolvables algébriquement.

Si $c > 0$ , alors $e^{u} = c ⟺ u = \ln (c)$	Si $c > 0$ , alors $e^{u} < c ⟺ u < \ln (c)$
Si $c \leq 0$ , alors l'équation $e^{u} = c$ n'a pas de solution.	Si $c \leq 0$ , alors l'inéquation $e^{u} < c$ n'a pas de solution. Si $c \leq 0$ , alors l'inéquation $e^{u} > c$ est toujours vraie.
$e^{u} = e^{v} ⟺ u = v$	$e^{u} < e^{v} ⟺ u < v$

Exercices :

Résolution guidée d'une inéquation du type \(c*e^{a x+b} > d)
Etude guidée du signe d'une expression du type \((a x+b)*e^{c x+d})
Etude guidée du signe d'une expression du type \(c*e^{a x+b} + d)

Remarque :
En dehors des cas précédents, on ne sait en général pas résoudre une (in)équation avec exponentielle par le calcul algébrique.
On peut parfois, par un changement de variable, se ramener à une équation polynomiale résoluble algébriquement.
Sinon, on utilise une méthode de résolution approchée. En général, on se ramène à résoudre l'équation

f (x) = 0

. On étudie les variations de la fonction

f

; on localise les éventuelles solutions en appliquant le théorème de la bijection dans des intervalles bien choisis ; puis on encadre chaque solution à une précision voulue au moyen de la calculatrice...

7. Primitives

Théorème : Soit

u

une fonction dérivable sur un intervalle

I

.
La fonction

f = u' e^{u}

admet comme primitives toutes les fonctions

F = e^{u} + C

où

C

est une constante réelle, et seulement celles-ci.

Une primitive de

f : x \mapsto e^{a x}

est donc

F : x \mapsto \frac{e^{a x}}{a}

(pour

a \neq 0

)

Exemples (cliquer sur l'icône pour changer les données) :
Soit $f$ la fonction définie sur par $f (x) = - 10 e^{}$ .
Alors $f$ admet comme primitive la fonction $F$ définie par : $F (x) = e^{}$ .
Toute autre primitive $G$ de $f$ s'écrit : $G (x) = F (x) + C = e^{} + C$ où $C$ est une constante réelle.

Exercice :

Primitives d'une exponentielle

résumé de cours sur la fonction exponentielle.
: functions, exponential, interactive mathematics, interactive math, server side interactivity

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.