OEF ЖрЯюЪН
--- НщЩм ---
БОФЃПщФПЧААќКЌ 32 ИіЙигкЪЕЛђИДЯЕЪ§ЕЅБфСПЖрЯюЪНЕФСЗЯА:
Иљ, ДЮЪ§, ИДКЯ, ДјгрГ§ЗЈ, ...
гыЕМЪ§ЕФзюДѓЙЋвђЪНДЮЪ§
Щш P(x) ЪЧвЛИі ДЮЯЕЪ§ЖрЯюЪН, Ыќга ИіВЛЭЌЕФЪЕИљКЭ ИіВЛЭЌЕФИДИљ (ВЛМЦжиЪ§). Щш P'(x) ЪЧ P(x) ЕФЕМЪ§. ЮЪ gcd(P(x),P'(x)) ЕФДЮЪ§ЪЧЖрЩй?
гажиИљЕФзюаЁДЮЪ§
ТњзувдЯТЬѕМўЕФЯЕЪ§ЖрЯюЪН P(x) ЕФзюаЁДЮЪ§ЪЧЖрЩй? ШчЙћФуШЯЮЊетбљЕФЖрЯюЪНВЛДцдк. дђЛиД№ -1.
КЭЕФДЮЪ§
Щш () КЭ () ЪЧСНИіЖрЯюЪН. ЮЪ: Шє deg()= МА deg()=, дђ ЪЧвЛИіЖрЯюЪН, ЫќЕФДЮЪ§ЮЊ
ВюЗжЗНГЬ
ЧѓЖрЯюЪН () ЪЙЕУ ()-() = 2 Чв ()=.
ЮвУЧгУ x^3 ДњБэ 3, ШчДЫРрЭЦ.
3 ДЮЖрЯюЪНЕФжиИљ
вдЯТЖрЯюЪНгавЛИіжиИљ. ЪдЧѓГіетИіИљ.
4 ДЮЖрЯюЪНЕФжиИљ
вдЯТЖрЯюЪНгавЛИіжиИљ. ЪдЧѓГіетИіИљ.
5 ДЮЖрЯюЪНЕФжиИљ
вдЯТЖрЯюЪНгавЛИіжиИљ. ЪдЧѓГіетИіИљ.
6 ДЮЖрЯюЪНЕФжиИљ
вдЯТЖрЯюЪНгавЛИіжиИљ. ЪдЧѓГіетИіИљ.
вбжЊгыЕМЪ§ЕФзюДѓЙЋвђЪН
ЧѓГіЖрЯюЪН () ЪЙЕУ: - gcd((),()) = ()() , етРя () ЪЧ () ЕФЕМЪ§;
- ()= ;
- ЕФДЮЪ§ОЁПЩФмаЁ.
ФуЪфШыЕФЖрЯюЪНаДГЩвђЪНГЫЛ§ЛђеЙПЊЕФаЮЪНОљПЩНгЪм. ЮвУЧгУ x^3 ДњБэ 3, ШчДЫРрЭЦ.
вбжЊ3ДЮЖрЯюЪНЕФИљ
ЧѓЖрЯюЪН P() = 32 , вбжЊ КЭ ЪЧЪЕЪ§, ЪЧвЛИіИљ.
гы2НзЕМЪ§ЕФзюДѓЙЋвђЪНЕФзюаЁДЮЪ§
Щш P(x) ЪЧвЛИі ДЮЯЕЪ§ЖрЯюЪН, Ыќга ИіВЛЭЌЪЕИљгы ИіВЛЭЌИДИљ (ВЛМЦжиЪ§). Щш P''(x) ЪЧ P(x) ЕФ 2 НзЕМЪ§. ЮЪзюДѓЙЋвђЪН gcd(P(x),P''(x)) ДЮЪ§ЕФзюаЁжЕЪЧЖрЩй?
гыИпНзЕМЪ§ЕФзюДѓЙЋвђЪНЕФзюаЁДЮЪ§
Щш P(x) ЪЧвЛИі ДЮЯЕЪ§ЖрЯюЪН, Ыќга ИіВЛЭЌЪЕИљгы ИіВЛЭЌИДИљ (ВЛМЦжиЪ§). Щш P()(x) ЪЧ P(x) ЕФ НзЕМЪ§. ЮЪзюДѓЙЋвђЪН gcd(P(x),P()(x)) ДЮЪ§ЕФзюаЁжЕЪЧЖрЩй?
3 ДЮЖрЯюЪНИљЕФжиЪ§
ЪЧвдЯТЖрЯюЪНЕФвЛИіИљ. ЧѓЫќЕФжиЪ§.
4 ДЮЖрЯюЪНИљЕФжиЪ§
ЪЧвдЯТЖрЯюЪНЕФвЛИіИљ. ЧѓЫќЕФжиЪ§.
5 ДЮЖрЯюЪНИљЕФжиЪ§
ЪЧвдЯТЖрЯюЪНЕФвЛИіИљ. ЧѓЫќЕФжиЪ§.
6 ДЮЖрЯюЪНИљЕФжиЪ§
ЪЧвдЯТЖрЯюЪНЕФвЛИіИљ. ЧѓЫќЕФжиЪ§.
3 ДЮКЌВЮЪ§ЖрЯюЪНЕФжиИљ
Чѓ
ЕФвЛИіжЕЪЙвдЯТЖрЯюЪНгавЛИіжиИљ, ВЂЧѓГіетИіжиИљ.
ОЏИц. БОСЗЯАЕФЛиД№жаВЛФмгаНќЫЦЪ§! НтЖМЪЧећЪ§. евевПД.
4 ДЮКЌВЮЪ§ЖрЯюЪНЕФжиИљ
Чѓ
ЕФвЛИіжЕЪЙвдЯТЖрЯюЪНгавЛИіжиИљ, ВЂЧѓГіетИіжиИљ.
ОЏИц. БОСЗЯАЕФЛиД№жаВЛФмгаНќЫЦЪ§! НтЖМЪЧећЪ§. евевПД.
2ДЮВЮЪ§ЗНГЬ
ВЮЪ§ ШЁЪВУДЪЕЪ§жЕЪБ, ЖрЯюЪН ()2 + (2) + га? (МйЩш 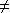 0.)
0.)
2ДЮВЮЪ§ЗНГЬ II
ВЮЪ§ ШЁЪВУДЪЕЪ§жЕЪБ, ЖрЯюЪН ()2 + () + () гавЛИіИљ ? (МйЩш 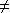 0.)
0.)
2ДЮЖрЯюЪНЕФИДИљ
ЧѓвдЯТЖрЯюЪНЕФСНИіИљ P() = 2 + () + (). Иљ , ЕФДЮађПЩвдШЮвт.
2ДЮЖрЯюЪНИљЕФКЏЪ§
Щш , ЪЧвдЯТЖрЯюЪНЕФ 2 ИіИљ 2 , Цфжа ЪЧЪЕЪ§. ЮЪ t = 2+2 ЕФжЕЪЧЪВУД? (етИіжЕЪЧ ЕФКЏЪ§.)
3ДЮЖрЯюЪНИљЕФКЏЪ§
Щш , , ЪЧвдЯТЖрЯюЪНЕФ 3 ИіИљ 3 2 , Цфжа ЪЧЗЧСуЪЕЪ§. ЮЪ t = ЕФжЕЪЧЪВУД? (етИіжЕЪЧ ЕФКЏЪ§.)
2ДЮЖрЯюЪНИљЕФЪЕВП
Щш P() = 2 + ЪЧгавЛЖдЙВщюИДИљЕФЪЕЯЕЪ§ЖрЯюЪН. ЮЪИљ r ЕФЪЕВПЪЧЪВУД?
гУЕМЪ§МЦЫуИљЕФИіЪ§
Щш P(x) ЪЧ ДЮЯЕЪ§ЖрЯюЪН, ЧвЩш P'(x) ЪЧ P(x) ЕФЕМЪ§. вбжЊ gcd(P(x),P'(x)) ЪЧвЛИі ДЮЖрЯюЪН. ЮЪ P(x) ЕФВЛЭЌЕФИљЕФИіЪ§ЪЧЖрЩй? (АќРЈЪЕИљгыИДИљ)
ИДКЯЖрЯюЪНЕФИљ
Щш () ЪЧЖрЯюЪН, () = 2 ЪЧСэвЛЖрЯюЪН. ПМТЧИДКЯЖрЯюЪН (()) КЭ (()). ЬюПе: Шє ЪЧ ЕФвЛИіИљ, дђ.
2ДЮЖрЯюЪНЕФЪЕИљ
ЧѓвдЯТЖрЯюЪНЕФСНИіИљ r1, r2
2 . (ИљЪЧЪЕЪ§, ДЮађВЛМЦ.)
КЭЛђЛ§ЕФИљЕФжиЪ§
Щш () КЭ () ЪЧСНИіЖрЯюЪН. ЬюПе: Шє ЪЧ () ЕФ жиИљвВЪЧ () ЕФ жиИљ, дђ ЪЧ ЕФ ________ жиИљ.
2ДЮЖрЯюЪНИљЕФЧщПі
вдЯТЖўДЮЖрЯюЪНгадѕбљЕФИљ? 2
Ш§ЯюЪНЕФвђЪНЗжНт
вђЪНЗжНт
.
Ек 1 ВН. ФуАб
ЯюЛЏГЩЭъШЋЦНЗН:
= (
)2.
ЮвУЧга
.
Ек 2 ВН. Ыљвд
Ыљвд
Ек 3 ВН.
ЯждкЮвУЧгІгУЙЋЪН
(
)(
).
НсЙћ:
.
(ФугІИУЪфШыЛЏМђКѓЕФБэДяЪН.)
3ДЮЖрЯюЪНЕФШ§жиИљ
дквдЯТЖрЯюЪНРяВЮЪ§ КЭ ШЁЪВУДЪЕЪ§жЕЪБЛсгаШ§жиИљ P() = 3 + 2 + + (-) ?
3ДЮЖрЯюЪНЕФШ§жиИљ II
дквдЯТЖрЯюЪНРяВЮЪ§ КЭ ШЁЪВУДЪЕЪ§жЕЪБЛсгаШ§жиИљ P() = 3 2 +(++) ? (ПЩгаЖрИіНт.)
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaюtre votre navigateur web.
Veuillez noter que les pages WIMS sont gщnщrщes interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent ъtre utilisщes interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: ЙигкЪЕЛђИДЯЕЪ§ЕЅБфСПЖрЯюЪНЕФвЛзщСЗЯА. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, algebra, polynomial,root,euclidean division,gcd,lcm,complex number
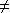 0.)
0.)
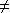 0.)
0.)
 0.)
0.)